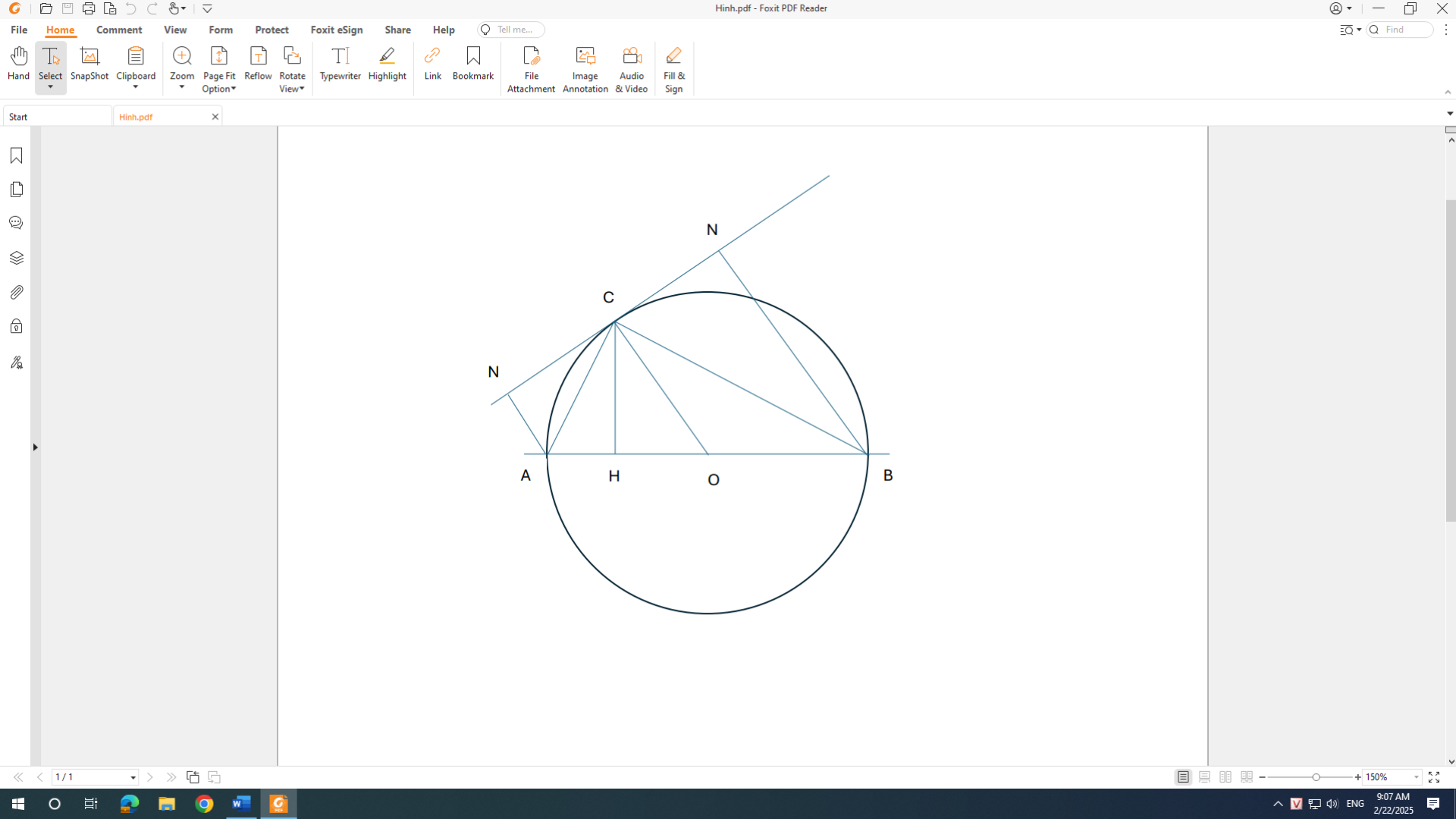
(Đề bài phải sửa thành c/m \(CH^2=AH.BH\) )

Xét tg vuông AHC có

\(CH^2=AC^2-AH^2\) (Pitago) (1)

Xét tg vuông BCH có

\(CH^2=BC^2-BH^2\) (Pitago) (2)

Cộng 2 vế của (1) và (2)

\(\rArr2CH^2=AC^2+BC^2-\left(AH^2+BH^2\right)\)

\(\lrArr2CH^2=AC^2+BC^2-\left(AH+BH\right)^2+2AH.BH\)

\(\lrArr2CH^2=AC^2+BC^2-AB^2+2AH.BH\)

Xét tg ACB có

\(\hat{ACB}=90^{o}\) (Góc nt chắn nửa đường tròn)

\(\rArr AC^2+BC^2=AB^2\) (Pitago)

\(\rArr2CH^2=2AH.BH\)

\(\rArr CH^2=AH.BH\)

Ta có

AM⊥d (gt); OC⊥d (gt); BN⊥d (gt) => AM//OC//BN

\(\rArr\frac{CM}{CN}=\frac{OA}{OB}=1\rArr CM=CN\)

=> OC là đường trung bình của hình thang AMNB

\(\rArr OC=\frac{AM+BN}{2}\rArr AM+BN=2OC\) Không đổi

=> AM.BN lớn nhất khi AM=BN

Khi đó tứ giác AMNB có

AM//BN (cmt); AM=BN => AMNB là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Mà AM⊥d (gt)

=> AMNB là HCN => AM⊥AB; mà AM//OC => OC⊥OB

=> sđ \(\overgroup{AC}\) = sđ\(\overgroup{BC}\) (Trong hình tròn đường kính vuông góc với dây cung thì chia đôi cung bị chắn)

=> AM.BN đặt giá trị lớn nhất khi C là điểm giữa của cung AB

\(a,b-b,a=3,6\)

\(\rArr\overline{}a+0,1xb-b-0,1xa=3,6\)

\(\lrArr0,9xa-0,9xb=3,6\)

\(\lrArr a-b=3,6:0,9=4\)

\(\lrArr a+b=4+2b\)

a+b lớn nhất khi b lớn nhất

Từ \(a-b=4\rarr a=b+4\le9\rarr b\le5\)

=> b lơn nhất khi b=5

Khi đó \(a=b+4=5+4=9\)

a+b lớn nhất bằng

9+5=14

\(\lrArr a^2-b^2=117\)

\(\lrArr\left(a-b\right)\left(a+b\right)=117=3.39=9.13\) (1)

Ta có

\(\left(a+b\right)-\left(a-b\right)=2b>0\rArr a+b>a-b\)

(1)\(\lrArr\left[\begin{array}{l}\begin{cases}a-b=3\\ a+b=39\end{cases}\\ \begin{cases}a-b=9\\ a+b=13\end{cases}\end{array}\right.\)

=> a+b là số nguyên tố

n-3⋮5 => 2(n-3)=2n-6=(2n-1)-5⋮5 => 2n-1⋮5

n-4⋮7 => 2(n-4)=2n-8=(2n-1)-7⋮7 => 2n-1⋮7

n-5⋮9 => 2(n-5)=2n-10=(2n-1)-9⋮9 => 2n-1⋮9

Để n nhỏ nhất thỏa mãn đề bài thì

2n-1=BCNN(5,7,9)=315

=> n=(315+1):2=158

\(\frac{3n^2+5}{n-1}=3n+3+\frac{8}{n-1}\)

Để \(3n^2+5\) chia hết cho \(n-1\) thì 8 phải chia hết cho n-1

\(\rArr\left(n-1\right)=\left\lbrace-8;-4;-2;-1;1;2;4;8\right\rbrace\)

\(\rArr n=\left\lbrace-7;-3;-1;0;2;3;5;9\right\rbrace\)

|------|------|------|------| Tổng 4 số

|------|--| Số a

Tổng 3 số là

25+35+52=112

Nhìn trên sơ đồ đoạn thẳng ta thấy 3 lần TBC của 4 số là

112+5=117

TBC của 4 số là

117:3=39

Số a là

9+5=14

\(3b=3+3^2+3^3+\cdots+3^{2013}\)

\(2b=3b-b=3^{2013}-3^{o}=3^{2013}-1\)

\(\rArr2b+1=3^{2013}\)

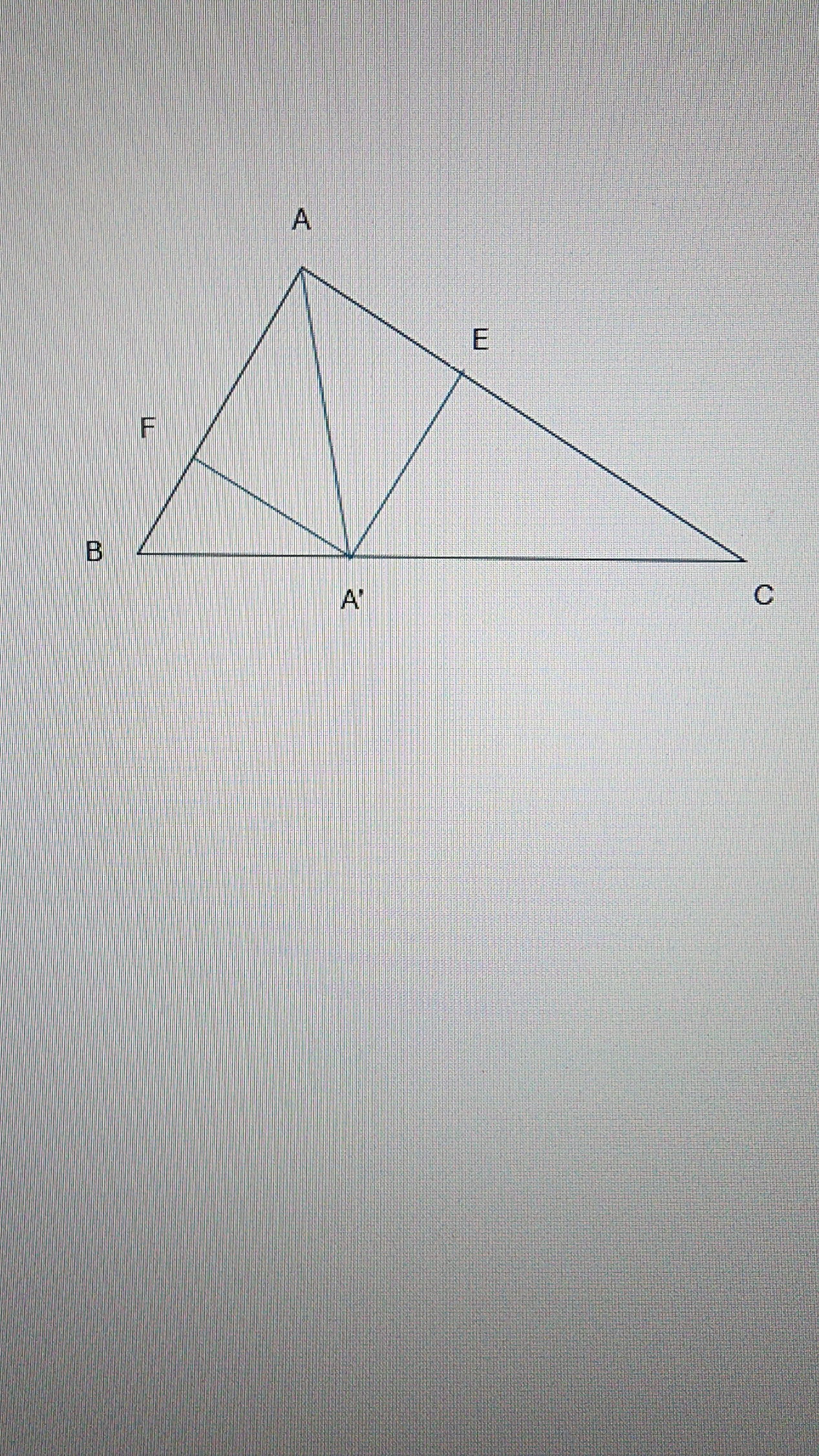
Xét △ABC

AB⊥AC (gt); A'E⊥AC (gt) => A'E//AB (cùng vg với AC)

\(\rArr\frac{CE}{AC}=\frac{A^{\prime}C}{BC}\) (1)

A'F⊥AB (gt); AC⊥AB (gt) => A'F//AC (cùng vg với AB)

\(\rArr\frac{BF}{AB}=\frac{A^{\prime}B}{BC}\) (2)

Chia 2 vế của (1) cho (2)

\(\rArr\frac{CE}{AC}.\frac{AB}{BF}=\frac{A^{\prime}C}{A^{\prime}B}\rArr\frac{CE}{BF}.\frac{AB}{AC}=\frac{A^{\prime}C}{A^{\prime}B}\)

Ta có AA' là phân giác của \(\hat{A}\)

\(\rArr\frac{A^{\prime}C}{A^{\prime}B}=\frac{AC}{AB}\) (Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy)

\(\rArr\frac{CE}{BF}.\frac{AB}{AC}=\frac{AC}{AB}\rArr\frac{CE}{BF}=\frac{AC^2}{AB^2}\)

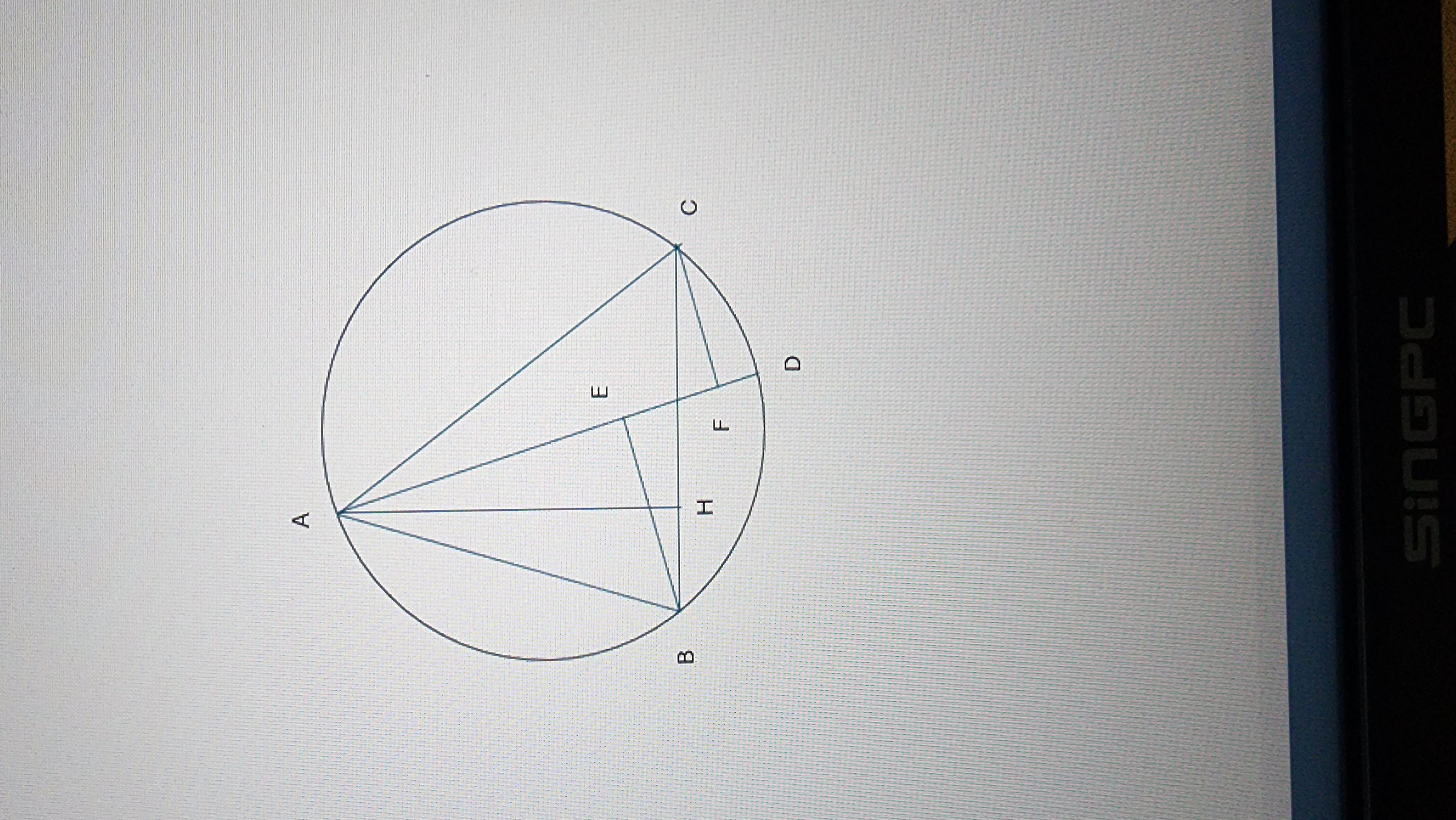
a/

AH⊥BC (gt) \(\rArr\hat{AHB}=90^{o}\)

BE⊥AD (gt) \(\rArr\hat{AEB}=90^{o}\)

H và E cùng nhìn AB dưới 2 góc = nhau và \(=90^{o}\)

=> ABHE là tứ giác nội tiếp

b/

Xét (O)

\(\hat{ACD}=90^{o}\) (góc nt chắn nửa đường tròn)

Xét tg vuông ABH

\(\hat{BAH}+\hat{ABC}=90^{o}\)

Xét tg vuông ADC

\(\hat{DAC}+\hat{ADC}=90^{o}\)

Mà \(\hat{ABC}=\hat{ADC}\) (Góc nt cùng chắn cung AC)

Xét tg vuông ABH và tg vuông ADC có

\(\hat{ABC}=\hat{ADC}\) (cmt)

=> tg ABH đồng dạng với tg ADC

\(\rArr\frac{BH}{DC}=\frac{AH}{AC}\rArr BH.AC=AH.DC\)

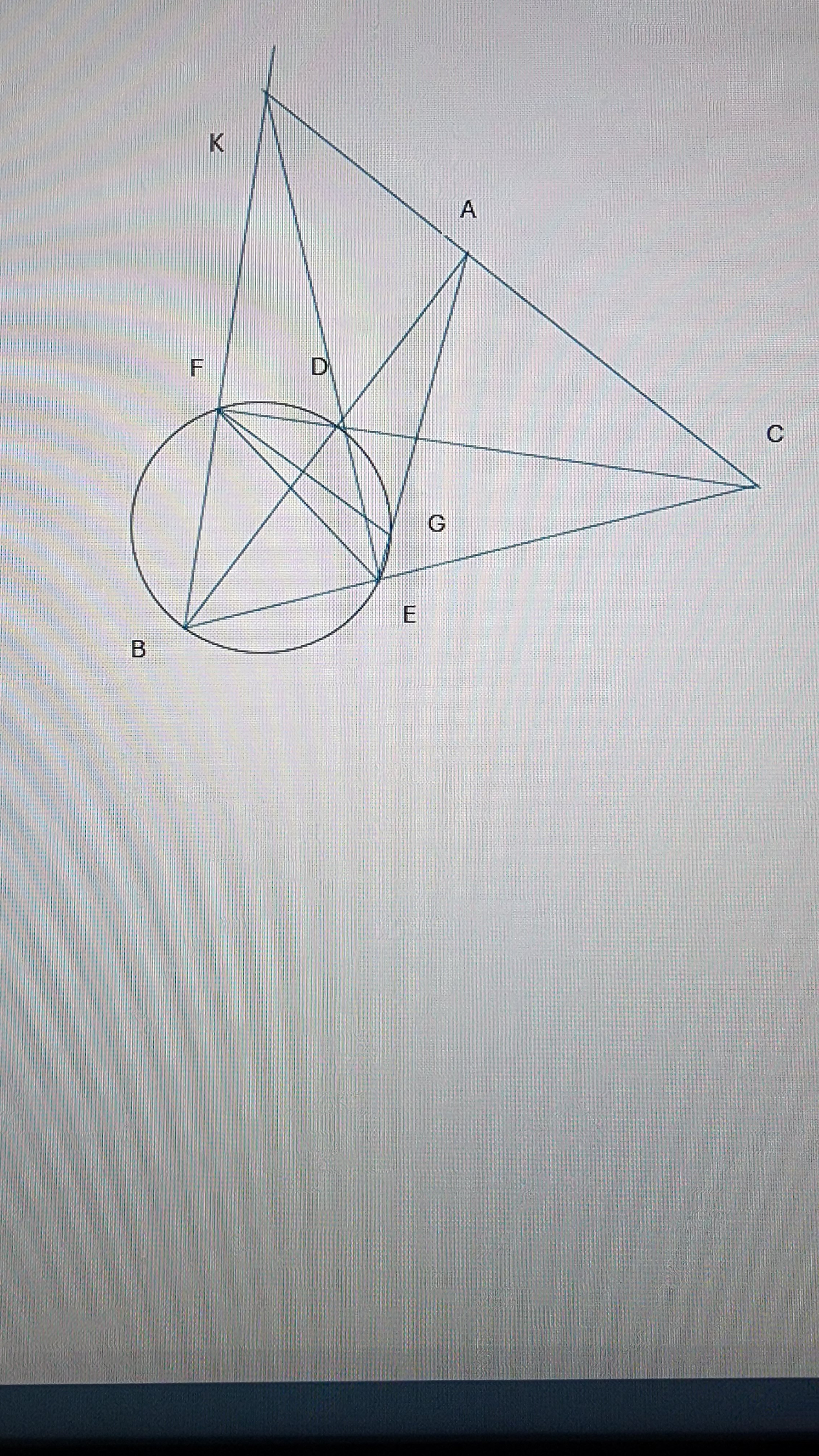
a/

Xét đường tròn đường kính BD

\(\hat{BED}=90^{o}\) (Góc nt chắn nửa đường tròn)

Xét tg vuông ABC và tg vuông EBD

\(\hat{ABC}\) chung

=> △ABC∼△EBD

b/

Ta có A và E cùng nhìn CD dưới 2 góc = nhau và \(=90^{o}\)

=> ADEC là tứ giác nt

Ta có

\(\hat{BFD}=90^{o}\) (Góc nt chắn nửa đường tròn)

=> A và F cùng nhìn BC dưới 2 góc = nhau và \(=90^{o}\)

=> AFBC là tứ giác nt

c/

Xét tứ giác nt ADEC

\(\hat{ACF}=\hat{AED}\) (góc nt cùng chắn cung AD)

Xét tứ giác nt AFBC

\(\hat{ACF}=\hat{ABF}\) (góc nt cùng chắn cung AF)

\(\rArr\hat{AED}=\hat{ABF}\)

Xét đường tròn đường kính BD

\(sđ\hat{AED}=\frac12sđcungDG\) ;\(sđ\hat{ABF}=\frac12sđcungDF\) (Góc nt)

\(\rArr sđcungDG=sđcungDF\)

\(sđ\hat{AED}=\frac12sđcungDF;sđ\hat{CFG}=\frac12sđcungDG\) (góc nt)

\(\rArr\hat{AED}=\hat{CFG}\) mà \(\hat{ACF}=\hat{AED}\) (cmt)

\(\rArr\hat{CFG}=\hat{ACF}\) , 2 góc này ở vị trí so le trong

=> AC//FG

d/

Gọi K là giao của AC với FB

Xét △KBC có

\(\hat{BFD}=90^{o}\) (cmt) => CF⊥KB

\(\hat{BAC}=90^{o}\) (gt) => BA⊥KC

=> D là trực tâm của △KBC

=> KD⊥BC

Mà \(\hat{BED}=90^{o}\) (cmt) => DE⊥BC

=> KD trùng DE (Từ 1 điểm bên ngoài 1 đường thẳng chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho)

=> AC; DE; FB đồng quy

e/ Gọi I là giao của FG với AB

Xét đường trong đường kính BD

\(\hat{BGD}=90^{o}\) (Góc nt chắn nửa đường tròn)

Xét tg vuông BFD và tg vuông BGD

\(sđcungDG=sđcungDF\) (cnt) => DF=DG (2 cung có số đo = nhau thì 2 dây trương cung bằng nhau)

BD chung

=> tg BFD = tg BGD (2 tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)

=> BF = BG => △BFG cân tại B

và \(\hat{DBF}=\hat{DBG}\)

=> BD⊥FG và IF = IG (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao và đường trung tuyến)

Xét △AFG có

BD⊥FG (cmt) => AD⊥FG; IF=IG (cmt) => △AFG cân tại A

\(\rArr\hat{DAF}=\hat{DAE}\) (trong tg cân đường cao xuất phát từ đỉnh tg cân đồng thời là đường phân giác) (1)

Xét đường tròn đường kính BD có

\(sđ\hat{FED}=\frac12sddcungDF;sđ\hat{AED}=\frac12sđcungDG\) (góc nt)

Mà \(sđcungDG=sđcungDF\) (cmt)

\(\rArr\hat{FED}=\hat{AED}\) (2)

Xét △AEF

Từ (1) và (2) => D là giao của 3 đường phân giác (trong tg 3 đường phân giác đồng quy)

=> D là tâm đường tròn nội tiếp △AEF