alligator -> cá sấu

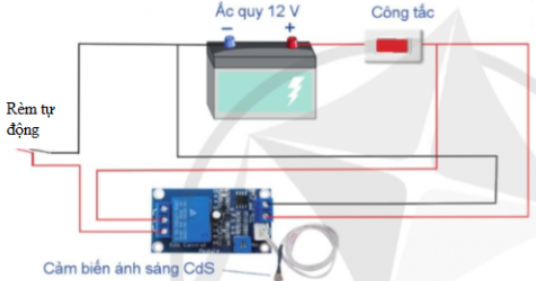
(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c

a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab

ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab

(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab

(a + b + c)x = (a + b + c)²

x = (a + b + c)²/(a + b + c)

x = a + b + c

Vậy S = {a + b + c}

a) Xét Δ𝐴𝐵𝐸ΔABE và Δ𝐴𝐶𝐹ΔACF có:

𝐵𝐴𝐶^BAC chung;

𝐴𝐸𝐵^=𝐴𝐹𝐶^=90∘AEB=AFC=90∘;

Do đó Δ𝐴𝐵𝐸∽Δ𝐴𝐶𝐹ΔABE∽ΔACF (g.g).

Suy ra 𝐴𝐵𝐴𝐶=𝐴𝐸𝐴𝐹ACAB​=AFAE​ nên 𝐴𝐵.𝐴𝐹=𝐴𝐶.𝐴𝐸AB.AF=AC.AE.

b) Từ 𝐴𝐵.𝐴𝐹=𝐴𝐶.𝐴𝐸AB.AF=AC.AE suy ra 𝐴𝐸𝐴𝐹=𝐴𝐵𝐴𝐶AFAE​=ACAB​.

Xét Δ𝐴𝐸𝐹ΔAEF và Δ𝐴𝐵𝐶ΔABC có:

𝐴𝐸𝐴𝐹=𝐴𝐵𝐴𝐶AFAE​=ACAB​ (cmt);

𝐵𝐴𝐶^BAC chung;

Do đó Δ𝐴𝐸𝐹∽Δ𝐴𝐵𝐶ΔAEF∽ΔABC (c.g.c)

Suy ra 𝐴𝐹𝐸^=𝐴𝐶𝐵^AFE=ACB (cặp góc tương ứng).

c) Xét Δ𝐶𝐸𝐵ΔCEB và Δ𝐶𝐷𝐴ΔCDA có:

𝐴𝐶𝐵^ACB chung;

𝐶𝐸𝐵^=𝐶𝐷𝐴^=90∘CEB=CDA=90∘

Do đó Δ𝐶𝐸𝐵∽Δ𝐶𝐷𝐴ΔCEB∽ΔCDA (g.g)

Suy ra 𝐶𝐵𝐶𝐸=𝐶𝐴𝐶𝐷CECB​=CDCA​ (cặp cạnh tương ứng).

Xét Δ𝐶𝐵𝐴ΔCBA và Δ𝐶𝐸𝐷ΔCED có:

𝐶𝐵𝐶𝐸=𝐶𝐴𝐶𝐷CECB​=CDCA​ (cmt);

𝐴𝐶𝐵^ACB chung;

Do đó Δ𝐶𝐵𝐴∽Δ𝐶𝐸𝐷ΔCBA∽ΔCED (c.g.c)

Suy ra 𝐶𝐷𝐸^=𝐶𝐴𝐵^CDE=CAB (cặp góc tương ứng) (1)

Tương tự: 𝐵𝐷𝐹^=𝐶𝐴𝐵^BDF=CAB (2).

Từ (1) và (2) suy ra 𝐶𝐷𝐸^=𝐵𝐷𝐹^CDE=BDF.

Mà 𝐶𝐷𝐸^+𝐸𝐷𝐴^=𝐵𝐷𝐹^+𝐹𝐷𝐴^CDE+EDA=BDF+FDA suy ra 𝐸𝐷𝐴^=𝐹𝐷𝐴^EDA=FDA.

Suy ra 𝐷𝐴DA là phân giác của góc 𝐸𝐷𝐹EDF.

Mặt khác 𝐴𝐷⊥𝐾𝐷AD⊥KD nên 𝐷𝐾DK là phân giác ngoài của Δ𝐷𝐸𝐹ΔDEF.

Ta có 𝐷𝐼DI là phân giác trong của Δ 𝐷𝐸𝐹Δ DEF suy ra 𝐼𝐹𝐼𝐸=𝐷𝐹𝐷𝐸IEIF​=DEDF​ (3)

Ta có 𝐷𝐾DK là phân giác ngoài của Δ𝐷𝐸𝐹ΔDEF suy ra 𝐾𝐹𝐾𝐸=𝐷𝐹𝐷𝐸KEKF​=DEDF​ (4)

Từ (3) và (4) suy ra 𝐼𝐹𝐼𝐸=𝐾𝐹𝐾𝐸IEIF​=KEKF​.

a) Với 𝑚=−1m=−1, hàm số trở thành 𝑦=−2𝑥+1y=−2x+1.

Xét hàm số 𝑦=−2𝑥+1y=−2x+1 :

Thay 𝑥=0x=0 thì 𝑦=1y=1.

Suy ra đồ thị hàm số 𝑦=−2𝑥+1y=−2x+1 đi qua điểm có tọa độ (0;1)(0;1).

Thay 𝑥=1x=1 thì 𝑦=−1y=−1.

Suy ra đồ thị hàm số 𝑦=−2𝑥+1y=−2x+1 đi qua điểm có tọa độ (1;−1)(1;−1).

Vẽ đồ thị:

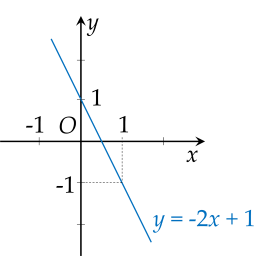
b) Vì đường thẳng (𝑑):𝑦=𝑎𝑥+𝑏(d):y=ax+b song song với đường thẳng (𝑑′ ):𝑦=−3𝑥+9(d′ ):y=−3x+9 nên: 𝑎≠−3;𝑏≠9a=−3;b=9.

Khi đó ta có: (𝑑):𝑦=−3𝑥+𝑏(d):y=−3x+b và 𝑏≠9b=9.

Vì đường thẳng (𝑑):𝑦=𝑎𝑥+𝑏(d):y=ax+b đi qua 𝐴(1;−8)A(1;−8) nên: −8=−3.1+𝑏−8=−3.1+b

Suy ra 𝑏=−5b=−5 (thoả mãn)

Vậy đường thẳng cần tìm là (𝑑):𝑦=−3𝑥−5(d):y=−3x−5.

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)

20 phút = 1/3 h

Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)

Quãng đường đi từ thành phố về quê: 30x (km)

Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)

Theo đề bài, ta có phương trình:

30x = 25(x + 1/3)

30x = 25x + 25/3

30x - 25x = 25/3

5x = 25/3

x = 25/3 : 5

x = 5/3 (nhận)

Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a) \(3x-5=4\). 3x=4+5 3x=9 x=9:3 x=3

1giờ 5 phút = 1,5 giờ

Quãng đường con ngựa chạy được là:

26 x 1,5 = 39 (km/giờ)

 Đáp số: 39 km/giờ

Điều quan trọng nhất là có thể kiểm soát được môi trường.